Mit Mathematik kann man viele tolle Dinge anstellen. Allerdings gibt es auch genug größere oder kleinere Themen, die einen (etwas) sehr verwirren können.
Russellsche Antimonie
Eines der bekanntesten Paradoxa ist die Russellsche Antinomie der naiven Mengenlehre. Erstmal ist die Frage, was die naive Mengenlehre eigentlich ist. Eine Menge M ist demnach eine Zusammenfassung von n wohlunterschieden Elementen zu einem Ganzen, zum Beispiel die Menge der natürlichen Zahlen von 1 bis 10.
Jetzt kommen wir aber zum Problem des Ganzen. Man kann sich mit dieser Definition sehr leicht in logische Widersprüche verstricken.
Einer der bekanntesten Widersprüche und gleichzeitig das Ende der naiven Mengenlehre kam mit der Russellschen Antimonie.
Bertrand Russell und Ernst Zermelo haben dieses Paradoxon als erstes erkannt.
Es geht um die Menge R, die alle Mengen enthält, aber sich nicht selbst als Element enthalten darf.
Also sprich wir haben unsere Menge R. Da sie alle Mengen enthalten soll, muss sie sich selbst enthalten, was sie aber nicht darf. Und wenn sie sich nicht selbst enthält, enthält sie auch nicht alle Mengen.
Hier ist also die Grenze der Erklärbarkeit durch die naive Mengenlehre erreicht, daraufhin wurde sie durch die axiomatische Mengenlehre ersetzt.
Hilberts Hotel

Ein weiterer mathematischer Begriff kann mit dem nächsten Fall veranschaulicht werden. Und zwar mit einem Hotel, welches voll belegt ist, aber immer noch Gäste aufnehmen kann.
Nun, dieses Hotel existiert nicht wirklich, ist aber ein sehr schönes Beispiel, wie komplex und unintuitiv die Unendlichkeit sein kann.
Die Idee kommt von dem Mathematiker David Hilbert. Hilberts Hotel ist ein Hotel mit unendlich vielen Zimmern, nummeriert von 1 fortlaufend. Nehmen wir an, jedes Zimmer ist belegt, aber mitten in einer kalten, stürmischen Nacht kommt jemand in das Hotel, in dessen Umfeld es offenbar keine weiteren Unterkünfte gibt und bittet komplett durchgefroren um ein Zimmer.
Der Portier bringt es nicht über das Herz denjenigen nicht weg zu schicken und überlegt, wie man ihn*sie am besten unterbringen kann.
Er geht zum Zimmer mit der Nummer 1 und bittet den Gast in das Zimmer 2 umzuziehen. Der Gast aus Zimmer 2 wird in das Zimmer 3 umquartiert und so weiter. Damit haben wir ein freies Zimmer gefunden.
Mathematisch heißt das also, dass jeder Gast aus Zimmer n in das Zimmer n+1 zieht.
Jetzt nehmen wir an, ein Bus hat vor unserem Hotel eine Panne und alle 30 Passagiere müssen untergebracht werden. Unser Portier hat inzwischen ja schon Übung darin und bittet alle Hotelbesucher*innen 30 Zimmer weiterzuziehen.
Zimmer n → Zimmer n+30
Jetzt wird es aber wieder kniffelig. Ein Bus mit unendlich vielen besetzten Sitzplätzen kommt zu dem Hotel. Wie bekommt man jetzt alle Personen einquartiert?
Nun, man bittet einfach jeden Gast in das Zimmer weiterzurücken, dessen Zimmernummer dem Doppelten seiner aktuellen entspricht.
Zimmer n → Zimmer 2*n
Dadurch werden alle Zimmer mit einer ungeraden Zimmernummer frei. Und da wir unendlich viele Zimmer haben, gibt es auch unendlich viele Zimmer mit ungerader Zimmernummer und der Portier kann alle Gäste unterbringen.
Was passiert aber, wenn unendlich viele Busse mit unendlich vielen Passagieren ankommen?
Das ist auch ganz einfach…
Wer aber wissen möchte wie das gelöst wird, der muss es sich entweder selbst überlegen (Primzahlen spielen eine wichtige Rolle) oder kann sich hier ein Video dazu anschauen, in dem der Sachverhalt von Anfang an noch mal sehr schön erklärt wird.
Allerdings muss man dazu sagen, dass wir hier nur den einfachsten Fall der Unendlichkeit betrachten, nämlich die natürlichen Zahlen. Wenn man dann noch mit den negativen, rationalen oder gar reellen Zahlen weitermacht, wird man beizeiten an die Grenzen des Erfassbaren stoßen.
Schlussendlich kann man sagen, dass man sehr schnell feststellt, dass die Unendlichkeit ein schwer greifbarer Begriff ist und man beim Nachdenken darüber durchaus in Sinnkrisen verfallen kann.
Geburtstagsparadoxon
Vielleicht wenden wir uns lieber noch einem etwas angewandteren Problem zu. Und zwar die Frage, wie hoch die Wahrscheinlichkeit ist, dass mindestens zwei Menschen einer Gruppe an dem selben Tag Geburtstag haben. Immerhin muss man sich dann einen Tag weniger merken.
Ich denke es ist klar, dass ab 366 Personen (unter Berücksichtigung des 29. Februars 367 Personen) mindestens 2 Menschen an dem gleichen Tag Geburtstag haben. Die Wahrscheinlichkeit liegt bei 1 bzw. 100%.
Doch wie sieht es bei einem gut besetzten Hörsaal mit 100 Personen aus?
Oder gar bei einem Seminar mit 25 Studierenden?

Bei 100 Personen liegt die Wahrscheinlich bei 99,99997 %.
Und selbst bei den 25 Menschen haben wir noch eine Wahrscheinlich von 56,87%.
Wer jetzt selbst mal rumspielen möchte, kann mit dieser Formel für beliebige Personenzahlen die Wahrscheinlichkeit bestimmen:
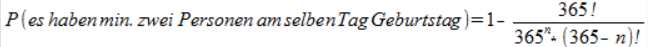
Ihr könnt ja mal in euren Vorlesung oder Seminaren nachfragen, ob es da auch einen Fall gibt.
Bildquellen:
Fragezeichen Bild von TeroVesalainen auf Pixabay
Birthdaycake Photo by Nick Stephenson on Unsplash
Hotel Photo by Marten Bjork on Unsplash




